40+ Sample Pythagorean Theorem Worksheet Templates
-

Pythagorean Theorem Worksheet
download now -
Revised Pythagorean Theorem Worksheet
download now -

Pythagorean Theorem Study Guide
download now -
Right Triangles and Pythagorean Theorem
download now -
Pythagorean Theorem Worksheet Template
download now -

Pythagorean Theorem – Worksheet
download now -

Sample Pythagorean Theorem Worksheet
download now -

Pythagorean Theorem Notes
download now -
Pythagorean Theorem
download now -
Pythagorean Theorem Quiz Review Sheet
download now -

Pythagorean Theorem Worksheet Sample
download now -

T-Chart Pythagorean Theorem
download now -

Pythagorean Theorem Word Problems
download now -

Pythagorean Theorem Quiz
download now -

Pythagoras Formula Worksheet
download now -

Pythagorean Theorem Student Worksheet
download now -

Pythagorean Theorem Worksheet Example
download now -
Pythagorean Theorem Homework
download now -

The Pythagorean Theorem Assignment
download now -
The Pythagorean Theorem
download now -
Worksheet – Pythagorean Theorem
download now -

Pythagorean Theorem Worksheet Format
download now -
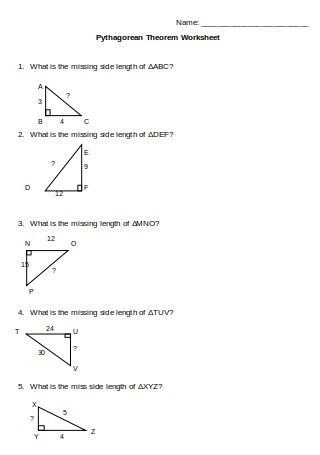
Pythagorean Theorem Worksheet in Word
download now -

Sample Pythagorean Theorem Study Guide
download now -

Pre-Algebra Pythagorean Theorem
download now -

Pythagorean Theorem – Worksheet in PDF
download now -

Pythagorean Theorem Practice
download now -

Independent Practice Worksheet
download now -

Best Pythagorean Theorem Worksheet
download now -

Geometry Pythagorean Theorem
download now -

Sample Pythagorean Theorem Word problems
download now -

Pythagorean Triples Worksheet
download now -
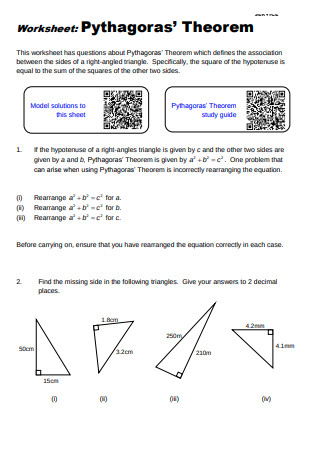
Pythagoras’ Theorem Worksheet
download now -
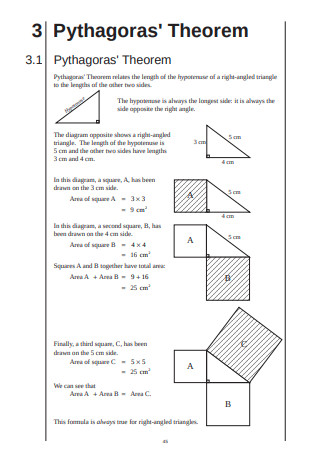
Pythagoras’ Theorem Template
download now -
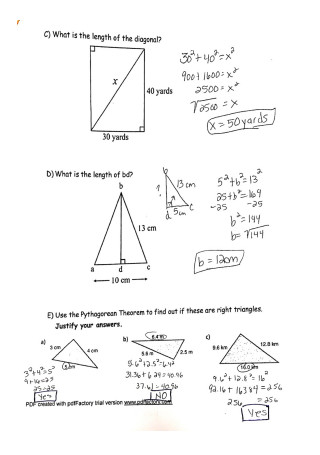
Pythagorean Theorem Assignment
download now -

Basic Pythagorean Theorem Worksheet
download now -

Pythagorean Theorem Lecture Notes
download now -
Pythagoras Theorem Lesson
download now -

Pythagorean Pythagorean
download now -
Pythagorean Theorem Sample Worksheet
download now -

Standard Pythagorean Theorem
download now
FREE Pythagorean Theorem Worksheet s to Download
40+ Sample Pythagorean Theorem Worksheet Templates
What is the Pythagorean Theorem?
Proving the Pythagorean Theorem
Advantage of Using Problem Sets
How to Solve for the Pythagorean Triangle
FAQs
Can I use the Pythagorean theorem with any triangle?
Can I use the Pythagorean theorem to find distance?
Who created the Pythagorean theorem?
What is the Pythagorean Theorem?
The formula a2+b2=c2 is to Math as “the mitochondrion is the powerhouse of the cell” is to Biology. The infamy of the Pythagorean theorem is not just because it is indefinitely reiterated to and by the students, since the day it was taught to them. The well-known formula is also the linchpin of subsequent higher mathematical disciplines. It is present in Geometry, fundamental in Trigonometry, and timeless in Physics. It is also useful in applications beyond the course Syllabus.
The Pythagorean theorem remains true for right triangles. A triangle is called a right triangle when one of its angles measures 90 degrees. Since the sum of all three angles in a triangle is 180 degrees, each of the two angles in a right triangle is always less than 90 degrees. Following this, the two sides of a right triangle that form the 90-degree angle are called the legs. The longest side that is opposite to the correct angle is called the hypotenuse. When you know the length of two sides of a right triangle, you can calculate for the third unknown length—as the general rule of the theorem, squaring, then adding the length of each leg will give you the square of the length of the hypotenuse. To find any missing range of the right triangle, you can play around with the formula.
In schools, teachers usually teach the theorem to students in the form of a diagram of a right triangle with one missing measurement. However, its real-world applications do not exist as a simple two-dimensional sketch of triangles. We are talking about construction, navigation, mapping, and the like. Being able to spout the formula at command alone shows little understanding of the concept. By including exercises and worksheets in their school workbooks, teachers can improve and augment the students’ comprehension of the Pythagorean theorem.
Proving the Pythagorean Theorem
In the academic community, rules generally do not last forever. Sometimes, new information can come to light and go against the present understanding of a case. This is how knowledge evolves with the times and mankind with it. Even though we have discarded a lot of the information from past studies due to recent development in science and technology, the old theorem still stands unrefuted. In fact, there are currently 367 mathematical proofs that support the Pythagorean theorem. The following are among the famous mathematical proofs.
Advantage of Using Problem Sets
It is not enough that students can memorize the formula or label a schematic accordingly. For students to appreciate the uses of the Pythagorean theorem, they should be acquainted with examples of its application. Instead of just answering direct questions, such as “Find c given the a and b values,” students should also solve word problems. Illustrate a real-world scenario for them that would require the use of the theorem. Word problems refine the students’ critical thinking. Translating questions into relatable story problems enable problem-solving Skills Development. In the real world, solutions will not be as obvious as a drawing of a triangle. Letting students use the concepts they learned in the classroom helps them develop a Strategy Mind Map for dealing with real-life problems. It also gives them the chance to appreciate what they are learning in school.
How to Solve for the Pythagorean Triangle
Should a problem require your students to use the Pythagorean formula in finding the missing value, they can follow the following step-by-step guide of solving the right triangle problem. For the following instructions, assume that the equation follows the following set-up: a2+b2=c2.
Step 1: Draw the Right Triangle
Although some people do not need to have a supplementary diagram, a beginner would need help in visualizing the problem. Illustrations are also an effective Teaching Strategy to keep students guided. Identify which are the legs and the hypotenuse. Before solving, you have to determine what is asked for in the problem. For good measure, always start each solution by writing the Pythagorean equation. As you become more familiar with the theorem, you won’t feel the need to rewrite the equation every time you solve for a missing value.
Step 2: Finding the Hypotenuse
If the problem is looking for the value of the hypotenuse, the equation is pretty straightforward. Start the solution by writing the equation with the unknown c2 on the other side of the equation. In the line below the equation, plug in the value for the legs a and b such that each value is placed inside a pair of parentheses, then add c2 after the equal sign. Don’t forget to add the superscript 2 after each closing parenthesis. In another line below, get the square of a and b separately. The square of a number is the number multiplied by itself. In the next line, add the squares. This time, remove by exponent 2 from c by placing the sum of the squares inside a square root symbol. Finally, the square root of the sum of squares is equals to the value of c.
Step 3: Solving for a or b
Things will go a little differently if a or b is the missing value. Suppose a is the missing length, and you have the values for b and c. In the following line, write a2 and plug in the given values into the original equation. Calculate for the squares of b and c. Now, you will one determined value on either side of the equation. Add to both sides of the equal sign the additive inverse of b. The additive inverse of an integer is its negative value, such that the sum of both is zero. Because of this, you are left with a2 on one side. You also have c plus negative b on the other side. Subtract b from c. Like last time, remove the exponent 2 from a by placing the other side inside a square root sign. The square root of the difference between c and b is equal to the value of a.
Step 4: Checking for Right Triangles
Some problems may not explicitly state that the triangle is a right triangle. Remember that the theorem governs calculations for right triangles. Firstly, a right triangle always has a 90-degree angle. But the problem or the diagram may not say so. You can use the principle learned from the Pythagorean theorem to determine if it is a valid approach in solving the problem. Calculate for the squares of each leg length of the triangle. After, combine the individual squares. Then, square the length of the hypotenuse. Finally, if the sum of the squares of the legs is equal to the square of the hypotenuse, you have got yourself a right triangle.
FAQs
Can I use the Pythagorean theorem with any triangle?
The Pythagorean theorem is unique and true only to triangles with a 90-degree angle. If you have a non-right triangle, you will have to resort to using the Cosine Law to solve for the missing values. The equation summarizes the Cosine Law is as follows: c2=a2 + b2– 2ab cos(C), where C is the angle opposite to the hypotenuse. In the case of right triangles where the angle C is 90, the cosine of C is equal to zero. Here, you will have the equation c2=a2 + b2– 0, which is analogous to the Pythagorean theorem. But when C is anything but 90 degrees, as is true for non-right triangles, you cannot generate the Pythagorean formula from the Cosine Law equation. You can use the law can for all types of triangles.
Can I use the Pythagorean theorem to find distance?
Yes. You can obtain the equation for finding the distance from the Pythagorean theorem. The distance between A and B on the plane is the square root of (x1?x2)2 + (y1?y2)2. You can use the distance formula when you have the x and y coordinates of the two points on the Cartesian plane. After you plot the two points respectively forming a right triangle, the diagonal line that connects points A and B is the hypotenuse. Notice that the theorem and the distance formula both come in the form of a2+b2=c2. Without memorizing the distance formula, you can use the Pythagorean theorem equation to come up with the same answers.
Who created the Pythagorean theorem?
Contrary to the name, Pythagoras was not the author of the Pythagorean theorem. The text found on ancient Babylonian tablet, dating more a thousand years before Pythagoras was born, suggests that the underlying principle of the theorem was already around and used by earlier scholars. According to an article in Science Mag, historians speculate that the tablet is the earliest known indication of the use of trigonometry yet. Other studies also suggest that Egyptian surveyors have used ideas reminiscent of the theorem. This information suggests that different cultures from separate parts of the world had played with the concept and properties of right triangles. The theorem was named after Pythagoras after he provided a strong proof of the theorem.
The Pythagorean theorem and related concepts would not be reiterated in classrooms if it had no bearing in the real world. However, there is a disconnect between its worldly application and how it is being taught inside the classrooms. Students can solve basic questions fine, but they falter on more complicated problems. By supplementing course learning with extensive classroom exercises through worksheets, students can gain a good foundation and working knowledge on the subject. At the end of the course material, you can evaluate your teaching approach by distributing Education Questionnaires. By improving your teaching methods one-course material at a time, Mathematics may become less intimidating in the future.
