Sample Proportion, PDF
-

Population and Sample Proportion
download now -

Proportion Method
download now -

Professional Proportion
download now -

Size for a Single Proportion
download now -

Sampling For Proportions and Percentages
download now -

Proportion and the Central Limit Theorem
download now -
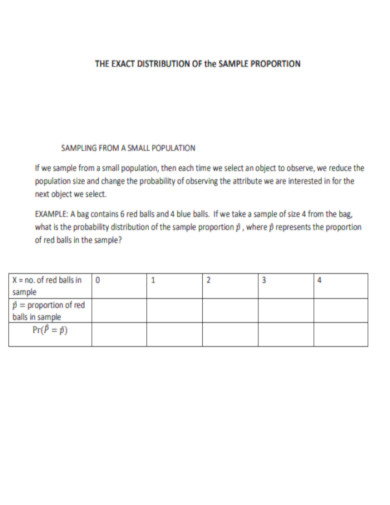
Exact Distribution of Proportion
download now -

Printable Proportion
download now -
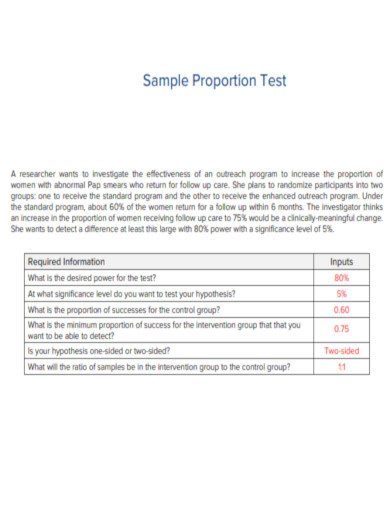
Proportion Test
download now -

Ratio Proportion
download now -

Sample Proportion and Variation
download now -

Practical Applications of Proportions
download now -

Proportion PDF
download now -

True Proportions
download now -

Tests for One Proportion
download now -

Mathematics Proportion
download now -

Writing Proportions
download now -

Concept of Proportion
download now -

Formal Proportion
download now -

Proportions Notes
download now -

Measurement of a proportion
download now -

Estimate Proportions
download now -

Statistical Analysis of Proportions
download now -

Direct Proportion
download now -

Proportion Practice
download now -

Single Proportion
download now -

General Proportion
download now -
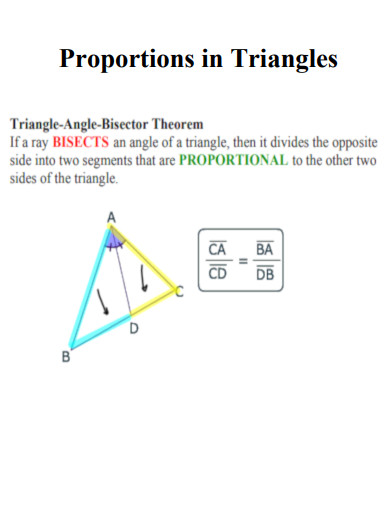
Proportions in Triangles
download now -

Inference About a Population Proportion
download now -

Proportions Using Cross Products
download now -

Proportions and Variation
download now -

Calculating Proportions
download now -

Solving Proportions
download now -

Standard Proportion
download now -

Percent Proportion
download now -

Design and the Divine Proportion
download now -

Proportion and Scale
download now -

Interval Estimation for a Binomial Proportion
download now -

Golden Proportion
download now -

Inferential Statistics for Proportions
download now -

Confidence Intervals for a Proportion
download now -

Basic Proportion
download now -

Ratio Proportion Partnership with Solutions
download now -

Expressing Proportions
download now -

Out of Proportion
download now -

Classifying Proportion and Non-proportion
download now -

Testing a Claim About a Proportion
download now -

Proportion Mapping the Conceptual Field
download now -
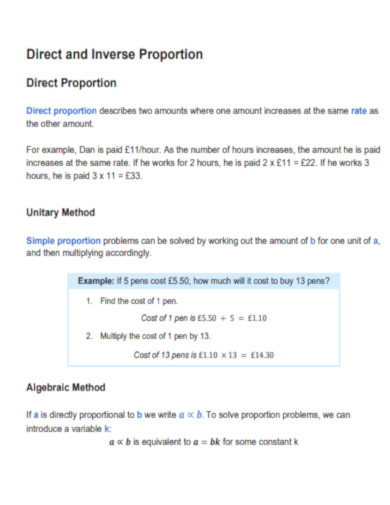
Direct and Inverse Proportion
download now -

Rational Expressions Proportions
download now -

Proportion Worksheet
download now -

Modelling Spatially Sampled Proportion Processes
download now -

Estimated Proportion
download now
FREE Proportion s to Download
Sample Proportion, PDF
What Is a Sample Proportion?
Definitions of Concepts and Terms
Types of Proportions
How to Calculate Sample Proportion
FAQs
What is sample proportion in hypothesis testing?
What is the probability of a sample proportion?
How to interpret proportions in statistics?
How does sample proportion affect standard deviation?
What is the purpose of the sampling proportion?
What are the common types of sampling methods?
Why are sample proportion and sample mean unbiased?
What is the relationship between confidence interval and confidence level?
How to find the sample size for a confidence interval proportion?
What Is a Sample Proportion?
The sample proportion (p̂) defines the proportion of individuals in a sample with a specific characteristic or trait. As a statistic and random variable denoted with a capital P or (P̂), the sample proportion varies from sample to sample in one way or another that cannot be predicted with certainty. It has a mean (μPˆ) and a standard deviation (σPˆ). Being used in statistics and survey research, it may equal the population proportion, or it may not. When researchers and statisticians work with large samples, the sample proportion is almost normally distributed, with mean μPˆ=p and standard deviation σPˆ=pq/n.
For example, if each face of an ordinary dice has an equal chance of landing on top when it is rolled, it is considered fair or balanced. So, the proportion of times a three evident in a huge number of tosses is expected to be approximately ⅙ or 0.16. Suppose the sample proportion of 0.15 came from rolling the dice 2,400 times instead of only 240 times. The probability that a fair dice would create a proportion of 0.15 or less is 0.0139. To interpret this result, a sample proportion of 0.15 or less in only about 1.14% is expected of all samples of size 2,400, indicating a piece of solid evidence that the dice is not fair.
Definitions of Concepts and Terms
There are numerous concepts and terms related to proportion tests used in statistics and survey research. Be well-informed on the useful definitions of these terms so that you can easily work on your sampling methods and other essential tools to accomplish your research.
Types of Proportions
Generally, proportions are based on ratios (a:b) and fractions (a/b). These concepts are integral in business, mathematics, and statistics. What are the different types of proportions?
1. Direct Proportion
It defines the direct relationship between two quantities. Simply, if one quantity increases, the other quantity increases as well. If you are dealing with quantities that are directly related or in direct proportion, use this rule. For instance, 24 x 240 = 12 x 480.
2. Inverse Proportion
It portrays the indirect relationship between two quantities. So, if one quantity increases, the other one decreases, or when the absolute value or magnitude of one variable gets bigger, the absolute value or magnitude of another variable gets smaller. This type of proportion is written as y ∝ 1/x.
3. Compound Proportion
This type of proportion involves two or more quantities. The quantities could be directly related or inversely related or both. There are some rules to compute compound proportion depending on the cases you are working on. If the first quantity and second quantity are directly related and the second quantity and third quantity are also directly related, then the formula is a x b/ c = d x e /x. If the first quantity and second quantity are directly related and the second quantity and third quantity are inversely related, the formula is b x c/a=e x x/d.
4. Continued Proportion
This type of proportion is when an ordered set of numbers like the ratio between any two successive terms is the same or if the ratio between the first and the second is equal to the ratio between the second and the third one. For example, a, b, and c are in continued proportion, if a : b = b : c.
How to Calculate Sample Proportion
Use the sampling distribution of the sample proportion to calculate the probability that your sample proportion lies within a specific range: P(p₁ < p̂ < p₂), P(p₁ > p̂), or P(p₁ < p̂). Thus, use the sample size (n), population proportion (p), and the specified proportions range. If you are not aware of the required sample size, use an effective sample size calculator.
Step 1: Understand the Sample Proportion Symbol
Familiarize yourself with the symbol of the sample proportion which is denoted by p̂. Count how many successes or characteristics of interest possessed by an individual are in the sample. Divide it by the total sample size.
Step 2: Draw Charts and Graphs
Construct charts and graphs and insert the fundamental data while calculating your sample proportion. Notice that different samples can provide you with different sample proportions. Plot the frequencies of each sample proportion in a histogram so that you can easily observe the behavior of the sample proportion.
Step 3: Check the Conditions for the Sampling Distribution of Proportions
To help you fully estimate the population proportion for the sampling distribution of proportions, you need to carefully check two conditions: randomization condition and independence or 10% condition. The randomization condition is when you check that your data comes from randomly selected samples. The independence condition is when you make sure that the sampled values are independent one from another. You need to consider sample sizes no larger than 10% of the whole population.
Step 4: Find the Mean and Standard Deviation for Sample Proportions
If you need to find the mean and standard deviations for a sample proportion, use the mean and standard deviation formula by calculating the mean or the simple average of the numbers. For each number, subtract the mean and square the result. Measure the mean of those squared differences and take the square root.
FAQs
The sample proportion in hypothesis testing, also known as the one-sample proportion test, is used to calculate an estimation of a population proportion. It sets a comparison of the proportion to a target or reference value and measures a range of values that is mostly to add the proportion of a population.
The probability of a sample proportion is 50% as long as the sampling distribution of the population proportion is symmetrical.
Statisticians and survey researchers use the p-value to identify whether the population proportion is statistically different from the hypothesized proportion.
The standard deviation decreases when the sample size increase since the sample size appears in the denominator of the square root.
The sampling proportion is carried out to estimate a population proportion that has a particular characteristic or trait.
The common types of sampling methods are cluster sampling, convenience sampling, purposive sampling, stratified sampling, probability sampling, systematic sampling, and many others.
The sample proportion and sample mean are unbiased because they aim at the parameters. Based on the rule, if the distribution center equals the true population value or the parameter, the distribution is identified as unbiased.
The confidence level refers to the percentage of times you anticipate getting near to the same estimate if you conduct your study again or repeat the population sample similarly. The confidence interval contains the upper and lower bounds of the estimate you anticipate t0 search at a given confidence level.
To find the sample size for population means, use this formula: n=(z×σE)2. On the other hand, use n=p×(1−p)×(zE)2 to find the sample size for population proportions.
What is sample proportion in hypothesis testing?
What is the probability of a sample proportion?
How to interpret proportions in statistics?
How does sample proportion affect standard deviation?
What is the purpose of the sampling proportion?
What are the common types of sampling methods?
Why are sample proportion and sample mean unbiased?
What is the relationship between confidence interval and confidence level?
How to find the sample size for a confidence interval proportion?
Whether you are one of the market researchers or survey analysts, a sample proportion is a crucial and valuable method to use, especially if you are conducting a survey or an experiment in a large target group or when everyone is involved in the study. Remember the definitions of the concepts, terms, and other components related to proportion tests such as population proportion, confidence level, and standard deviation, as well as the formulas to calculate the mean and standard deviation for sample proportions. To assist you in your statistics and survey research, check out other templates for survey analysis reports, survey forms, market research business plans, and market research reports.
