Sample Unit Circle Charts & Diagrams
-
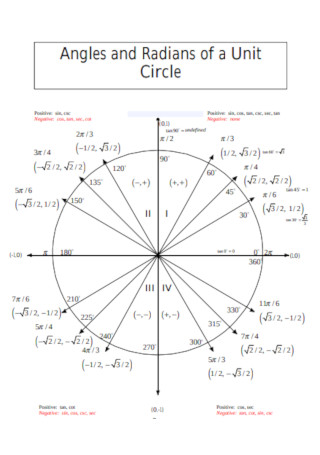
Radians of a Unit Chart Template
download now -
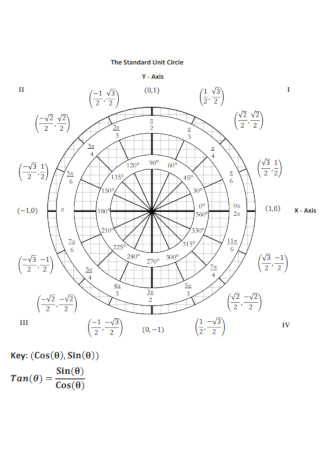
Academic Unit Circle Chart Template
download now -

Construction Unit Circle Chart Template
download now -

Math Unit Circle Chart Template
download now -
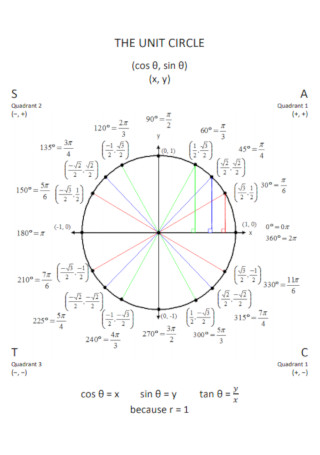
Simple Unit Circle Chart Template
download now -

Sample Unit Circle Trigonometry Template
download now -
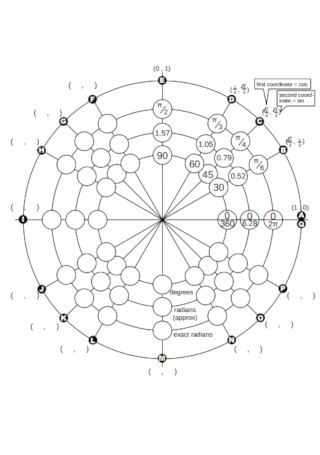
Formal Unit Circle Chart
download now -

Standard Unit Circle Chart Template
download now -

Printable Unit Circle Chart
download now -
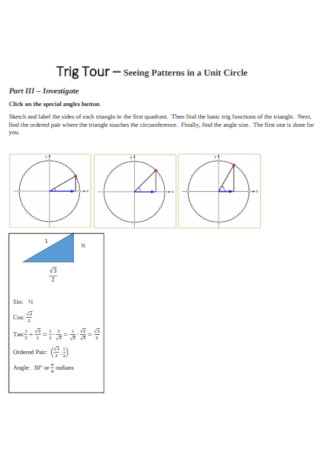
Trig Tour for unit Circle Template
download now -

Unit Circle Trigonometry Chat Template
download now -

Simple Unit Circle Diagram Example
download now -

Unit Circle Trig Function Diagram Template
download now -
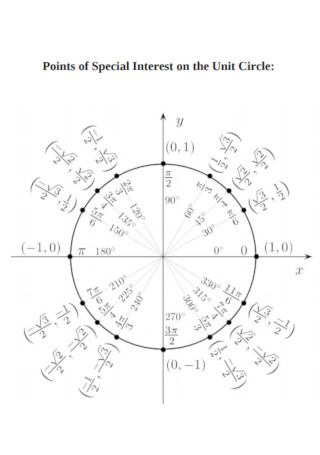
Points of Special Interest on the Unit Circle Diagram
download now -

Trigonometry Fundamentals and the Unit Circle Diagram Template
download now -
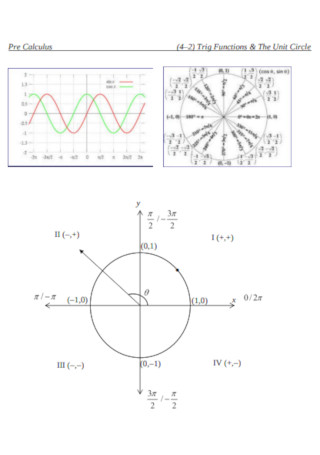
Unit Circle Pre Calculus Diagram Template
download now -
Prtintable unit Circle Diagram Template
download now -

Formal Unit Circle Diagram Example
download now -

Unit Circle Best Friend Diagram Template
download now -

Unit Circle Arclength Diagram Template
download now
FREE Unit Circle Chart & Diagram s to Download
Sample Unit Circle Charts & Diagrams
What Are Unit Circle Charts & Diagrams?
What Are the Different Trigonometric Identities?
How to Apply Trigonometry in Real Life?
How to Use a Unit Circle Diagram?
FAQs
Where did the unit circle come from?
How many quadrants does a unit circle have?
What is a reference angle?
Can a reference angle be negative?
Why is the unit circle important in Trigonometry?
What Are Unit Circle Charts & Diagrams?
A unit circle diagram is a tool used by mathematicians, teachers, and students like you to easily solve for sine, cosine, and the tangent of an angle of a triangle. This is a circle that consists of a radius that is equivalent to 1, which means that any straight line you draw from the circle’s center point up to its edge, will always be equivalent to 1. Furthermore, this circle has an x and y-axis intersecting in the middle, separating its negative and positive quadrants, serving as your guide in calculating for the cosine, sine, and tangent of any angle from 0° to 360° (also equivalent to 0 and 2? radians).
What Are the Different Trigonometric Identities?
Trigonometric identities are essential when you wish to simplify mathematical expressions related to trigonometric functions, especially with its equations valid for right-angled triangles. Some of these trigonometric identities are listed below:
How to Apply Trigonometry in Real Life?
Trigonometry is not just a simple study of triangles, lengths, heights, and angles. It also has a lot of functions in real life. In fact, this made a significant impact on the development under the fields of Engineering, aviation, astronomy, and many more that require familiarization of sines and cosines to create an output.
- Trigonometry in Engineering and Architecture – under the fields of engineering and architecture, trigonometry helps measure the height of the building, its distance, as well as its elevation to provide a safer place for its clients and a more comfortable and attractive structure.
- Trigonometry in Aviation – in aviation, pilots study and practice trigonometry to master how to manage the speed, direction, and distance of their airplane. They do this while taking into account the direction and strength of the wind, as well as the weather during each flight. By calculating the factors in navigating a plane, they are able to send their passengers safely from one place to another.
- Trigonometry in Cartography and Navigation – cartographers also make use of trigonometry in navigating directions as well as estimating and scaling the area to map the area. In doing so, they are able to provide explorers, tourists, and drivers accurate information in the area not only in paper written maps but also in GPS navigations.
- Trigonometry in Criminology – being an investigator, a police officer, or a criminologist may sound like a fun and exciting job. But did you know that they use trigonometry to solve cases and to catch criminals? With trigonometry, they are able to calculate the trajectory of a projectile and estimate the direction of the gunshot or even the cause of a collision of a car accident, helping them to solve their investigation in no time.
- Trigonometry in Marine Biology – marine biologists do not automatically dive into the depths of the ocean without knowing the terrain below. By using trigonometry, they are able to measure and estimate the depths of sunlight affecting the specimens under the water, the tools they need for the exploration, as well as the behavior and patterns of the creatures underneath.
How to Use a Unit Circle Diagram?
There are different ways to solve for cosine, sine, and tangent of a right triangle. You can solve it using a scientific calculator, or you may use the Pythagorean equation. However, what if you don’t have your calculator with you? How are you going to answer your exam? Well, there is another simpler way to do it. If you are studying trigonometry or calculus, how familiar are you with the unit circle? A unit circle can help you solve for the sine, cosine, and tangent of an angle by merely familiarizing yourself with its different coordinates. Find out more about how to use the unit circle and read these few tips below.
Step 1: Familiarize Yourself with the Major Angles and Radians of the Unit Circle
The unit circle is composed of radians, degrees, and major angles. The first step is to familiarize yourself with them. A circle is equivalent to a total of 360 degrees and is divided into four quadrants, wherein each quadrant has a total value of 90 degrees and is further divided into 30 degrees, 45 degrees, and 60 degrees each. Make sure to remember them together with their radian equivalents as they will come in handy later.
Step 2: Identify the Different Quadrants of the Unit Circle
As stated earlier, a unit circle is divided into four quadrants. You have quadrant one, located at the right upper side of the circle, and your quadrant two located at the upper left side of the circle. On the other hand, your quadrant three is located on the lower left side, while your quadrant four is located at the lower right side of the circle. Each of these quadrants is created with your x and y-axis intersecting in the middle of the circle. Identify the different quadrants of the unit circle and keep in mind that each quadrant has an equivalent positive and negative value.
Step 3: Familiarize Yourself with the Coordinates of Point on Circle
Now that you know the different radians, degrees, angles, and quadrants that make up the unit circle, the next is to familiarize yourself with the various coordinates of points on the circle. Each of these coordinates has corresponding angle degrees and radians equivalent. Make sure to determine which quadrant has a positive and negative x and y-axis since your x-coordinates are equivalent to your cosine while your y-coordinates are equivalent to your sine.
Step 4: Determine and Solve for Your Tangent
Lastly, now that you are familiar with the different parts of the unit circle, it’s time to solve for your tangent. Since your unit circle does not have a tangent, you need to use a formula to solve it. With your cosine and sine readily available in your unit circle, finding your tangent won’t take long. Simply use the method: tan? = sin? / cos? Keep these tips in mind, and you shall have no problem acing your math tests in no time.
FAQs
Where did the unit circle come from?
The unit circle, as well as Trigonometry, has been used by Egyptian mathematicians to build pyramids and Babylonian astronomers to keep track of stars and planets’ motion way back from the 2nd millennium BC. Later in history, Greek and Hellenistic mathematicians made use of the table of chords produced by Hipparchus, making him the father of Trigonometry. Soon, these were further developed and translated by various mathematicians around the world over time, until it was molded into the Trigonometry and unit circle from what you know it today.
How many quadrants does a unit circle have?
A unit circle is composed of four quadrants, namely, Quadrant I (QI), Quadrant II (Q II), Quadrant III (Q III), and Quadrant IV (Q IV). Quadrant one is composed of Both positive x and y coordinates (+X,+Y), Quadrant two is composed of negative and positive coordinates (-X,+Y). Quadrant three, on the other hand, is composed of both negative coordinates (-X,-X), while Quadrant four is composed of positive and negative coordinates (+X,-Y).
What is a reference angle?
A reference angle is a positive acute angle you find inside a unit circle that represents an angle of any measure. If you notice, this angle remains between 0 and 90 degrees, which makes it the smallest angle you find from the terminal side (where the angle ends) of the angle with the x-axis.
Can a reference angle be negative?
A quick answer is no, reference angle is always positive and is always less than or equal to 90 degrees, even for large angles regardless of which quadrant you place them since they always measure between 0 and 2.
Why is the unit circle important in Trigonometry?
Trigonometry is the study of triangles. Since the unit circle serves as a tool in helping you identify and calculate for the different trigonometric functions, which is one of the building blocks of the subject, it became essential in Trigonometry.
Now that you know what a unit circle is and what it’s used for, you are probably wondering what’s the point of learning all these cosines, sines, and tangents. If you don’t know, Trigonometry is a part of your life, especially when you work under the fields of engineering, astronomy, architecture, aviation, and criminology. When you use the unit circle to solve in Trigonometry, you are not merely solving for a missing side or angle of a triangle, but you are trying to identify and keep track of the trigonometry ratios and their relationships with one another. Trigonometry is never an easy subject, especially when you are still a beginner. Nevertheless, do not overthink and just have fun solving!
